Math Playground
Math Playground: Play with Math is an interactive, outdoor installation designed to transform abstract mathematical models and math thinking into engaging, larger-than-human playground equipment. Math is often perceived as difficult, abstract, or boring. Math playground makes math tangible, fun, and physically engaging. Visitors of all ages are invited to "play on the math"—climbing, sliding, swinging, and spinning on structures whose forms and mechanisms embody complex mathematical principles. Form follows function. The structure and the way people interact with it reveal the underlying math.
Form: Five distinct, custom-built playground equipment pieces situated within a public park setting. These sculptures are large-scale, durable, and safe installations that double as interactive public art. Math Playground invites people to play with math with their bodies, turning abstraction into embodied experience.
Much of the negative emotions expressed by the general public regarding mathematics comes from the belief that mathematics is a rigid system of arbitrary rules with only one correct way of arriving at a correct answer. This is rooted in the dominant narratives of mathematical philosophy established in the 19th and early 20th centuries, namely logicism and formalism, that downplays or outright ignores the role of play, intuition and entire histories of stumbles resulting in incremental refinements to a theory. In the 1970s, the mathematical philosopher Imres Lakatos shone a light on the view of mathematics as a human endeavor, with imperfect humans boldly making conjectures, proving and refining, with others poking holes in their theories through cleverly constructed counterexamples.
This playground is a manifestation of this more holistic, human and community-oriented approach to mathematics, one that celebrates the essential human role of creativity, exploration, experimentation and iteration. Symmetry is present not only in the beauty of forms but in how people mathematically play on the playground, translating through iterative practice, dilating large problems to smaller examples to gain better intuition, glide reflecting through moving forward and reflecting, moving forward and reflecting, and rotating around to gain new perspectives.
There are five sculptures in the playground:
1. Klein Bottle Slide
A looping tubular slide that creates the feeling of a continuous path. The design is inspired by the Klein bottle, a surface that has no inside or outside. Transparent sections allow riders to see how their path folds back into itself.
Math idea: A Klein bottle is a non-orientable surface where direction cannot be consistently defined. It is a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down.



2. Boy’s Surface Climbing Nets
A climbing net shaped from Boy’s surface. The net dips, bends, twists, and intersects so people can climb over and through it. Moving on the complex structure gives people a physical understanding of a surface that flips orientation.
Math idea: Boy's surface is the first known immersion of the real projective plane into three-dimensional space, a geometric shape with a complicated structure that has no edges and no points where the surface intersects itself.


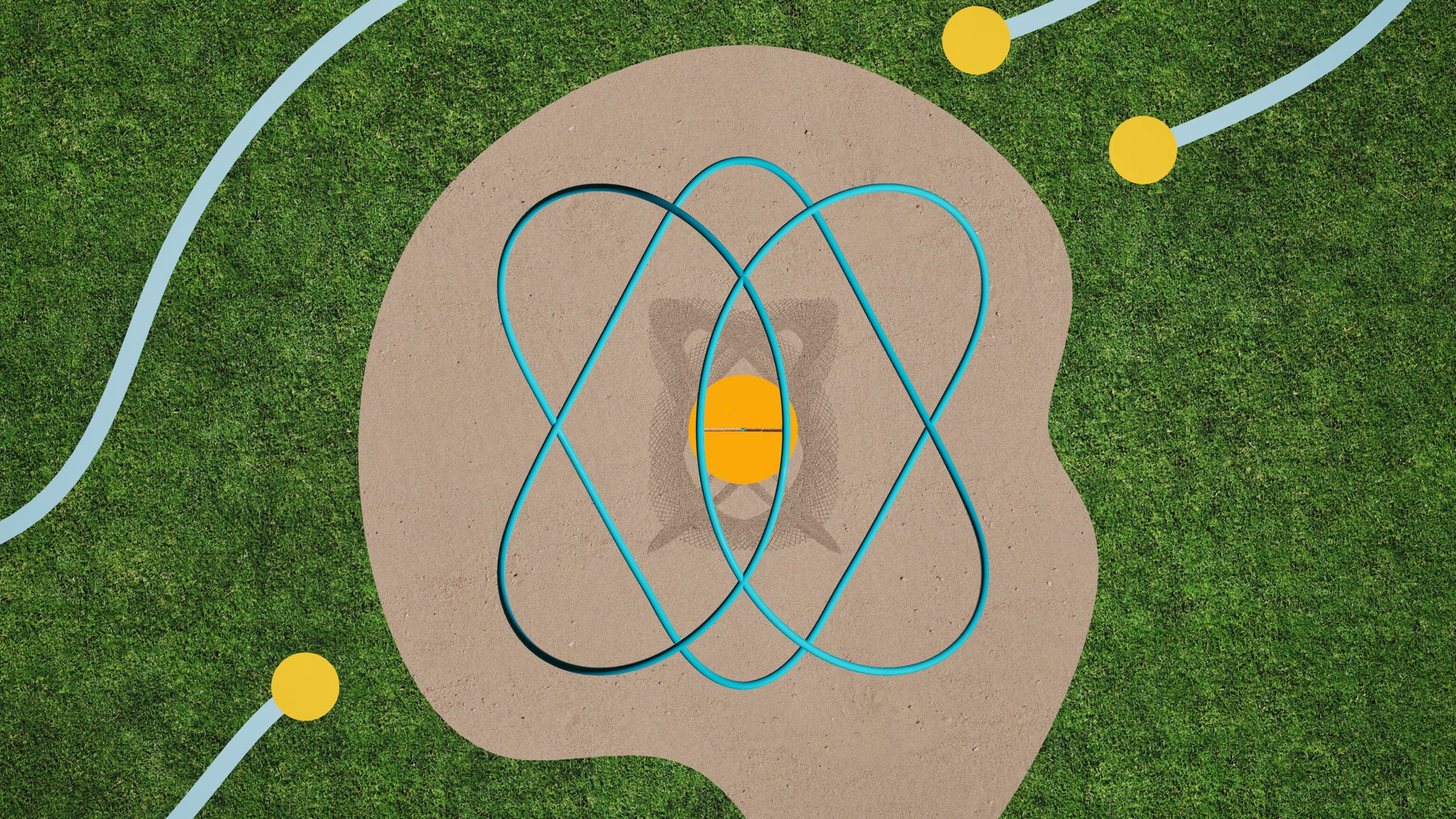
3. Lissajous Swing Set
Swings hang from two pivot points so each rider creates a Lissajous curve in the air. A small sandbag under the seat releases sand as the swing moves. The motion leaves patterns in the sand that look like flowers or knots. Each person creates a unique pattern because the curve depends on the person’s weight, the swinging rhythm and speed.
Math idea: Lissajous curves come from two oscillations happening at the same time. They visualize harmonic motion.

4. Merry-Go-Round Zoetrope
Inside the merry-go-round is a zoetrope. The inside wall contains a sequence of models and the outside has narrow slits. As the carousel spins, people sitting on it see the still models animate.
Math idea: A zoetrope uses periodic motion and evenly spaced frames to create the illusion of movement. It demonstrates rotation, repetition, and visual frequency.


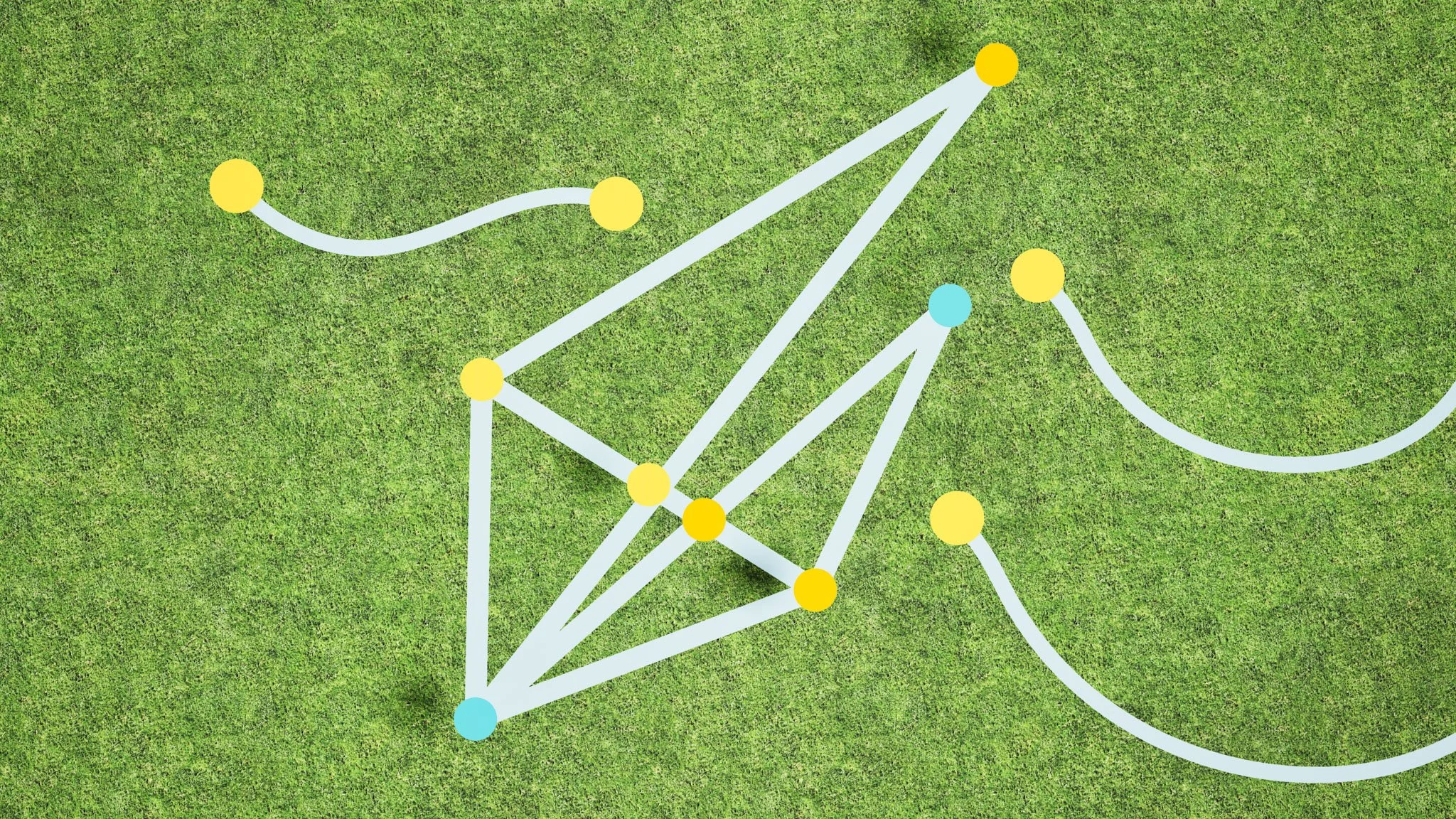
5. Euler Path Walkway
A network of paths connects all the playground structures. Visitors can choose their own route, with the challenge of passing by each piece exactly once without repeating a path.
Math idea: An Euler path is a route through a network that travels each connection exactly once.


Möbius strip seating
Jiabao Li, Fumiko Futamura, Ron Berry
Annan Zuo
Open Interval, Simons Foundation


